2.7. Fitting two different spectra simultaneously¶
Suppose one wants to fit two observed spectra from different sources (or areas on the sky) simultaneously with two different models, but with certain parameters coupled to each other. This is possible with SPEX! In this thread, we will guide you through the necessary steps to make this work.
2.7.1. Goal¶
Suppose we have two point sources absorbed by the same molecular cloud in front of them. The elemental abundances in the cloud appear to be non-solar, but are assumed to be constant trough the cloud. Let’s say, we want to fit both sources, while we couple the abundance in the absorber. This requires us to load two different spectra and apply two different source models to them, while constraining some parameters between the models.
2.7.2. Sectors and regions¶
Before we begin, it is good to understand the SPEX definitions of ‘sectors’ and ‘regions’. These SPEX concepts are very useful when creating more complicated fitting setups, but are often considered to be confusing. In this context, it is also useful to know the definition of ‘instruments’, because this is very close to the definition of ‘region’.
When fitting, SPEX needs to know which model (sector) needs to be applied to which observed spectrum (region).
This is already defined when spectra are converted to SPEX format with trafo, which is explained in the next
section.
2.7.3. Step 1: Trafo¶
For this science case, we have two sets of XMM-Newton MOS spectra: M1_src1.pha and M1_src2.pha and their
respective arf and rmf files. One spectrum for each point source.
To enable that we create two distinct models for each source, we need to set the relationship between the
model sectors that we will create later in SPEX and the spectra that we read in. In this case, we want the
model in sector #1 to be fitted to the observed spectrum #1 and, obviously, the model in sector #2 fitted to
observed spectrum #2. In SPEX, this needs to be defined already in the spectral file. For this, we use the
trafo program:
Linux:~> trafo
Program trafo: transform data to SPEX 2.0 format
This is version 1.04, of trafo
Are your data in OGIP format : type=1
Old (Version 1.10 and below) SPEX format: type=2
New (Version 2.00 and above) SPEX format: type=3
Enter the type: 1
In this example, we have OGIP files, so we enter 1 for the type. The next question is how many spectra
we want to transform and there we enter 2:
Enter the number of spectra you want to transform: 2
Enter the maximum number of response groups per energy per spectrum: 100000
Answer the next question with a large number, like 100000. The question after that is important for our purpose:
Enter the number of sectors you want to create: 2
Since we want to create two separate models, we enter 2 here. Then we can start to load the data one by one,
while defining the relation between the model number and observed spectrum at the same time. We start with source
number 1. For this source we define that sector (model) #1 should be fitted to spectrum (region) #1:
Enter the sector and region number: 1 1
After this, the usual trafo questions are asked about the input files. Provide trafo with the
files for source #1:
How should the matrix be partioned?
Option 1: keep as provided (1 component, no re-arrangements)
Option 2: rearrange into contiguous groups
Option 3: split into N roughly equal-sized components
Enter your preferred option (1,2,3): 1
Enter filename spectrum to be read: M1_src1.pha
Exposure time (s): 1.00000000E+04
Assuming Poissonian Errors
Areascal: 1.00000000E+00
Backscal: 1.00000000E+00
Backfile:
Corrscal: **************
Corrfile:
Respfile:
Ancrfile:
No background specified in pha-file.
Read nevertheless a background file? (y/n) [no]:
Checking data quality and grouping ...
Ogip files have quality flags. Quality 0 means okay
Your spectrum file has 0 bins with bad quality
Your combined file has 0 bins with bad quality
Shall we use these quality flags to ignore bad channels? (y/n) [no]:y
Your spectrum has grouping flags. Do you want your
Spectrum to be binned according to these groups? (y/n) [no]:n
Determining background subtracted spectra ...
No response matrix file specified in pha-file.
Enter filename response matrix to be read: M1_src1.rmf
Reading response matrix ...
Lower model bin boundary for bin 1 must be positive; current values: 0.000000E+00 5.000000E-03
Enter new bin boundary values manually: 3E-5 5E-3
Warning, ebounds data started at channel 0
Warning, response data started at channel 0
Possible response conflict; check xspec/spex with delta line!
Enter shift to response array (1 recommended, but some cases may be 0):1
No effective area file specified in pha-file.
Read nevertheless an effective area file? (y/n) [no]: y
Enter filename arf-file to be read: M1_src1.arf
Reading effective area ...
Determining zero response data ...
Total number of channels with zero response: 0
Original number of data channels : 800
Channels after passing mask and omitting zero response channels: 800
Rebinning data where necessary ...
Rebinning response where necessary ...
old number of response elements: 1280442
new number of response elements: 1280442
old number of response groups : 2394
new number of response groups : 2394
Correcting for effective area ...
Determine number of components ...
Found 1 components
Enter any shift in bins (0 recommended): 0
order will not be swapped ...
Now, we can do the same for source #2, but now we want model #2 to be fitted to spectrum #2:
Enter the sector and region number: 2 2
How should the matrix be partioned?
Option 1: keep as provided (1 component, no re-arrangements)
Option 2: rearrange into contiguous groups
Option 3: split into N roughly equal-sized components
Enter your preferred option (1,2,3): 1
Enter filename spectrum to be read: M1_src2.pha
Exposure time (s): 1.00000000E+04
Assuming Poissonian Errors
Areascal: 1.00000000E+00
Backscal: 1.00000000E+00
Backfile:
Corrscal: **************
Corrfile:
Respfile:
Ancrfile:
No background specified in pha-file.
Read nevertheless a background file? (y/n) [no]: n
Checking data quality and grouping ...
Ogip files have quality flags. Quality 0 means okay
Your spectrum file has 0 bins with bad quality
Your combined file has 0 bins with bad quality
Shall we use these quality flags to ignore bad channels? (y/n) [no]:n
Your spectrum has grouping flags. Do you want your
Spectrum to be binned according to these groups? (y/n) [no]:n
Determining background subtracted spectra ...
No response matrix file specified in pha-file.
Enter filename response matrix to be read: M1_src2.rmf
Reading response matrix ...
Lower model bin boundary for bin 1 must be positive; current values: 0.000000E+00 5.000000E-03
Enter new bin boundary values manually: 3E-5 5E-3
Warning, ebounds data started at channel 0
Warning, response data started at channel 0
Possible response conflict; check xspec/spex with delta line!
Enter shift to response array (1 recommended, but some cases may be 0):1
No effective area file specified in pha-file.
Read nevertheless an effective area file? (y/n) [no]: y
Enter filename arf-file to be read: M1_src2.arf
Reading effective area ...
Determining zero response data ...
Total number of channels with zero response: 0
Original number of data channels : 800
Channels after passing mask and omitting zero response channels: 800
Rebinning data where necessary ...
Rebinning response where necessary ...
old number of response elements: 1280442
new number of response elements: 1280442
old number of response groups : 2394
new number of response groups : 2394
Correcting for effective area ...
Determine number of components ...
Found 1 components
Enter any shift in bins (0 recommended): 0
order will not be swapped ...
Finally, we need to provide the file names for the .spo and .res files (M1):
Enter filename spectrum to be saved (without .spo): M1
Enter filename response to be saved (without .res): M1
Final number of response elements: 2560884
We now have the observed spectra in a data file that we can use in SPEX.
2.7.4. Step 2: SPEX¶
Let’s first load the data into SPEX and see how they look:
Linux:~> spex
Welcome user to SPEX version 3.06.00
Currently using SPEXACT version 2.07.00. Type `help var calc` for details.
SPEX> data M1 M1
SPEX> plot dev xs
SPEX> plot type data
SPEX> plot x log
SPEX> plot y log
SPEX> pl rx 0.4:10
SPEX> pl ry 1E-4:10.
SPEX> pl
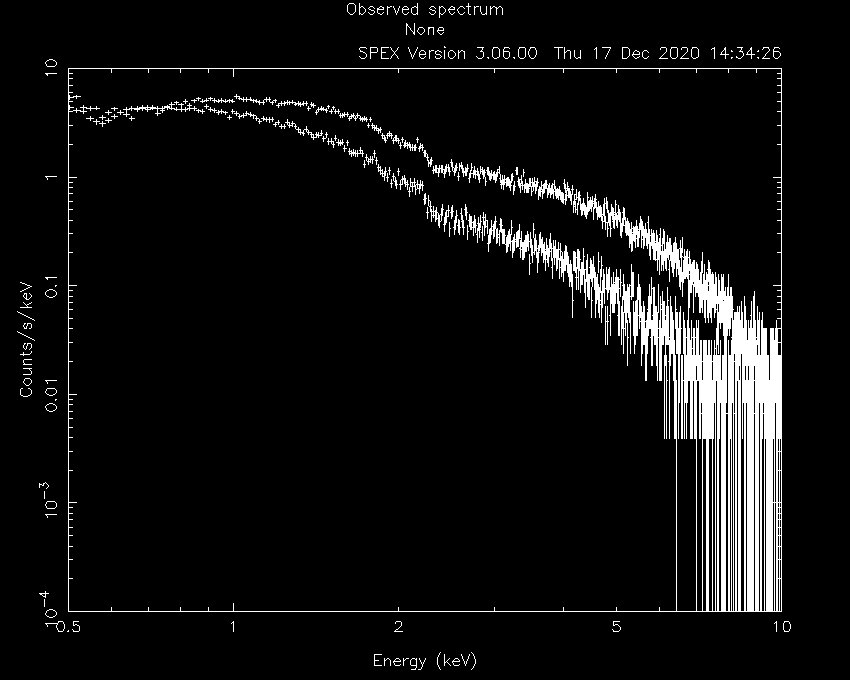
Now, we ignore the parts of the spectra that are not well calibrated or contain too little photons:
SPEX> ign 0.0:0.4 un k
SPEX> ign 10:100 un k
To keep this thread focused on the method to fit two different spectra, we chose to keep the models simple. Both sources consist of an absorbed powerlaw (with different slope and normalisation), but both absorbed by the same molecular cloud. Now, we need to define the model for both the sectors we intent to use:
SPEX> com hot
You have defined 1 component.
SPEX> com po
You have defined 2 components.
SPEX> com rel 2 1
SPEX> sector new
There are 2 sectors
SPEX> com 2 hot
You have defined 1 component.
SPEX> com 2 po
You have defined 2 components.
SPEX> com rel 2 2 1
SPEX> model show
--------------------------------------------------------------------------------
Number of sectors : 2
Sector: 1 Number of model components: 2
Nr. 1: hot
Nr. 2: pow [1 ]
Sector: 2 Number of model components: 2
Nr. 1: hot
Nr. 2: pow [1 ]
The absorption by the molecular cloud is done with the hot component and the power law using pow. Using
the model show command, we can see how the models are built up for each sector.
Note that in the case above, where the components in both sectors are the same, we could have used the command
sector copy to copy the contents of sector #1 into sector #2. This would have saved us a couple of lines
of commands.
Let’s have a look at how this shows in the par show command:
SPEX> par show
--------------------------------------------------------------------------------------------------
sect comp mod acro parameter with unit value status minimum maximum lsec lcom lpar
1 1 hot nh X-Column (1E28/m**2) 1.000000 thawn 0.0 1.00E+20
1 1 hot t Temperature (keV) 1.000000 thawn 2.00E-04 1.00E+03
1 1 hot rt T(balance) / T(spec) 1.000000 frozen 1.00E-04 1.00E+04
1 1 hot fcov Covering fraction 1.000000 frozen 0.0 1.0
1 1 hot v RMS Velocity (km/s) 100.0000 frozen 0.0 3.00E+05
1 1 hot rms RMS blend (km/s) 0.000000 frozen 0.0 1.00E+05
1 1 hot dv Vel. separ. (km/s) 100.0000 frozen 0.0 1.00E+05
1 1 hot zv Average vel. (km/s) 0.000000 frozen -1.00E+05 1.00E+05
1 1 hot ref Reference atom 1.000000 frozen 1.0 30.
1 1 hot 01 Abundance H 1.000000 frozen 0.0 1.00E+10
1 1 hot 02 Abundance He 1.000000 frozen 0.0 1.00E+10
1 1 hot 03 Abundance Li 1.000000 frozen 0.0 1.00E+10
1 1 hot 04 Abundance Be 1.000000 frozen 0.0 1.00E+10
1 1 hot 05 Abundance B 1.000000 frozen 0.0 1.00E+10
1 1 hot 06 Abundance C 1.000000 frozen 0.0 1.00E+10
1 1 hot 07 Abundance N 1.000000 frozen 0.0 1.00E+10
1 1 hot 08 Abundance O 1.000000 frozen 0.0 1.00E+10
1 1 hot 09 Abundance F 1.000000 frozen 0.0 1.00E+10
1 1 hot 10 Abundance Ne 1.000000 frozen 0.0 1.00E+10
1 1 hot 11 Abundance Na 1.000000 frozen 0.0 1.00E+10
1 1 hot 12 Abundance Mg 1.000000 frozen 0.0 1.00E+10
1 1 hot 13 Abundance Al 1.000000 frozen 0.0 1.00E+10
1 1 hot 14 Abundance Si 1.000000 frozen 0.0 1.00E+10
1 1 hot 15 Abundance P 1.000000 frozen 0.0 1.00E+10
1 1 hot 16 Abundance S 1.000000 frozen 0.0 1.00E+10
1 1 hot 17 Abundance Cl 1.000000 frozen 0.0 1.00E+10
1 1 hot 18 Abundance Ar 1.000000 frozen 0.0 1.00E+10
1 1 hot 19 Abundance K 1.000000 frozen 0.0 1.00E+10
1 1 hot 20 Abundance Ca 1.000000 frozen 0.0 1.00E+10
1 1 hot 21 Abundance Sc 1.000000 frozen 0.0 1.00E+10
1 1 hot 22 Abundance Ti 1.000000 frozen 0.0 1.00E+10
1 1 hot 23 Abundance V 1.000000 frozen 0.0 1.00E+10
1 1 hot 24 Abundance Cr 1.000000 frozen 0.0 1.00E+10
1 1 hot 25 Abundance Mn 1.000000 frozen 0.0 1.00E+10
1 1 hot 26 Abundance Fe 1.000000 frozen 0.0 1.00E+10
1 1 hot 27 Abundance Co 1.000000 frozen 0.0 1.00E+10
1 1 hot 28 Abundance Ni 1.000000 frozen 0.0 1.00E+10
1 1 hot 29 Abundance Cu 1.000000 frozen 0.0 1.00E+10
1 1 hot 30 Abundance Zn 1.000000 frozen 0.0 1.00E+10
1 1 hot file File electr.distrib.
1 2 pow norm Norm (1E44 ph/s/keV) 1.000000 thawn 0.0 1.00E+20
1 2 pow gamm Photon index 2.000000 thawn -10. 10.
1 2 pow dgam Photon index break 0.000000 frozen -10. 10.
1 2 pow e0 Break energy (keV) 1.0000000E+10 frozen 0.0 1.00E+20
1 2 pow b Break strength 0.000000 frozen 0.0 10.
1 2 pow type Type of norm 0.000000 frozen 0.0 1.0
1 2 pow elow Low flux limit (keV) 2.000000 frozen 1.00E-20 1.00E+10
1 2 pow eupp Upp flux limit (keV) 10.00000 frozen 1.00E-20 1.00E+10
1 2 pow lum Luminosity (1E30 W) 2.5786482E-02 frozen 0.0 1.00E+20
2 1 hot nh X-Column (1E28/m**2) 1.000000 thawn 0.0 1.00E+20
2 1 hot t Temperature (keV) 1.000000 thawn 2.00E-04 1.00E+03
2 1 hot rt T(balance) / T(spec) 1.000000 frozen 1.00E-04 1.00E+04
2 1 hot fcov Covering fraction 1.000000 frozen 0.0 1.0
2 1 hot v RMS Velocity (km/s) 100.0000 frozen 0.0 3.00E+05
2 1 hot rms RMS blend (km/s) 0.000000 frozen 0.0 1.00E+05
2 1 hot dv Vel. separ. (km/s) 100.0000 frozen 0.0 1.00E+05
2 1 hot zv Average vel. (km/s) 0.000000 frozen -1.00E+05 1.00E+05
2 1 hot ref Reference atom 1.000000 frozen 1.0 30.
2 1 hot 01 Abundance H 1.000000 frozen 0.0 1.00E+10
2 1 hot 02 Abundance He 1.000000 frozen 0.0 1.00E+10
2 1 hot 03 Abundance Li 1.000000 frozen 0.0 1.00E+10
2 1 hot 04 Abundance Be 1.000000 frozen 0.0 1.00E+10
2 1 hot 05 Abundance B 1.000000 frozen 0.0 1.00E+10
2 1 hot 06 Abundance C 1.000000 frozen 0.0 1.00E+10
2 1 hot 07 Abundance N 1.000000 frozen 0.0 1.00E+10
2 1 hot 08 Abundance O 1.000000 frozen 0.0 1.00E+10
2 1 hot 09 Abundance F 1.000000 frozen 0.0 1.00E+10
2 1 hot 10 Abundance Ne 1.000000 frozen 0.0 1.00E+10
2 1 hot 11 Abundance Na 1.000000 frozen 0.0 1.00E+10
2 1 hot 12 Abundance Mg 1.000000 frozen 0.0 1.00E+10
2 1 hot 13 Abundance Al 1.000000 frozen 0.0 1.00E+10
2 1 hot 14 Abundance Si 1.000000 frozen 0.0 1.00E+10
2 1 hot 15 Abundance P 1.000000 frozen 0.0 1.00E+10
2 1 hot 16 Abundance S 1.000000 frozen 0.0 1.00E+10
2 1 hot 17 Abundance Cl 1.000000 frozen 0.0 1.00E+10
2 1 hot 18 Abundance Ar 1.000000 frozen 0.0 1.00E+10
2 1 hot 19 Abundance K 1.000000 frozen 0.0 1.00E+10
2 1 hot 20 Abundance Ca 1.000000 frozen 0.0 1.00E+10
2 1 hot 21 Abundance Sc 1.000000 frozen 0.0 1.00E+10
2 1 hot 22 Abundance Ti 1.000000 frozen 0.0 1.00E+10
2 1 hot 23 Abundance V 1.000000 frozen 0.0 1.00E+10
2 1 hot 24 Abundance Cr 1.000000 frozen 0.0 1.00E+10
2 1 hot 25 Abundance Mn 1.000000 frozen 0.0 1.00E+10
2 1 hot 26 Abundance Fe 1.000000 frozen 0.0 1.00E+10
2 1 hot 27 Abundance Co 1.000000 frozen 0.0 1.00E+10
2 1 hot 28 Abundance Ni 1.000000 frozen 0.0 1.00E+10
2 1 hot 29 Abundance Cu 1.000000 frozen 0.0 1.00E+10
2 1 hot 30 Abundance Zn 1.000000 frozen 0.0 1.00E+10
2 1 hot file File electr.distrib.
2 2 pow norm Norm (1E44 ph/s/keV) 1.000000 thawn 0.0 1.00E+20
2 2 pow gamm Photon index 2.000000 thawn -10. 10.
2 2 pow dgam Photon index break 0.000000 frozen -10. 10.
2 2 pow e0 Break energy (keV) 1.0000000E+10 frozen 0.0 1.00E+20
2 2 pow b Break strength 0.000000 frozen 0.0 10.
2 2 pow type Type of norm 0.000000 frozen 0.0 1.0
2 2 pow elow Low flux limit (keV) 2.000000 frozen 1.00E-20 1.00E+10
2 2 pow eupp Upp flux limit (keV) 10.00000 frozen 1.00E-20 1.00E+10
2 2 pow lum Luminosity (1E30 W) 2.5786482E-02 frozen 0.0 1.00E+20
Instrument 1 region 1 has norm 1.00000E+00 and is frozen
Instrument 1 region 2 has norm 1.00000E+00 and is frozen
--------------------------------------------------------------------------------
Fluxes and restframe luminosities between 2.0000 and 10.000 keV
sect comp mod photon flux energy flux nr of photons luminosity
(phot/m**2/s) (W/m**2) (photons/s) (W)
1 2 pow 2.963082E-03 2.752802E-18 4.000000E+43 2.578606E+28
2 2 pow 2.963082E-03 2.752802E-18 4.000000E+43 2.578606E+28
--------------------------------------------------------------------------------
Fit method : Classical Levenberg-Marquardt
Fit statistic : C-statistic
C-statistic : 2929139.50
Expected C-stat : 64.11 +/- 16.31
Chi-squared value : 158042.30
Degrees of freedom: 0
W-statistic : 0.00
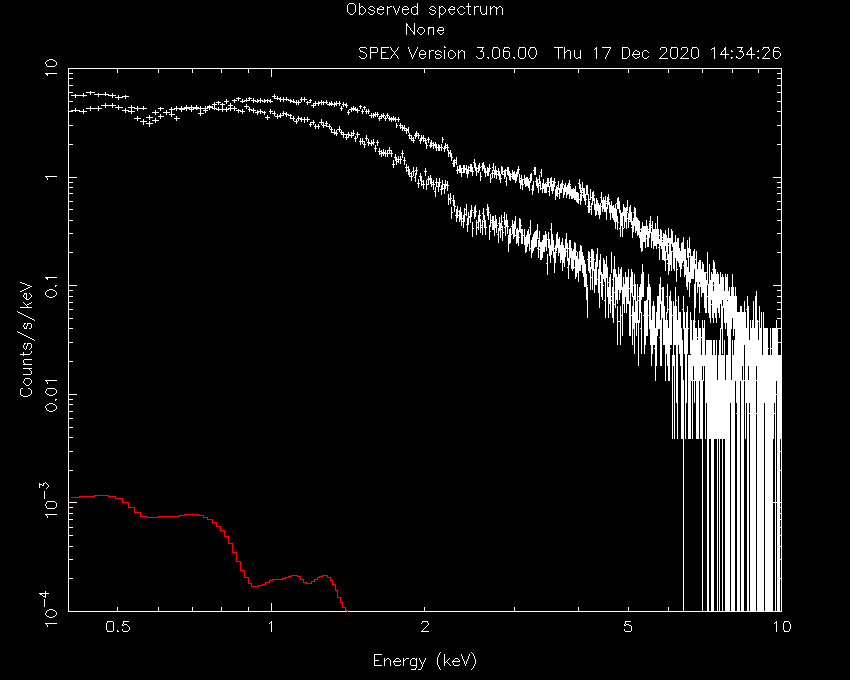
Obviously, the initial model parameters are quite far off. We also need to fix the hot model to a low temperature to mimic neutral gas:
SPEX> par 1 1 t v 2E-4
SPEX> par 2 1 t v 2E-4
SPEX> par 1 1 t stat f
SPEX> par 2 1 t stat f
SPEX> par 1 1 nh v 1E-3
SPEX> par 2 1 nh v 1E-3
SPEX> par 1 2 norm v 1000
SPEX> par 2 2 norm v 1000
SPEX> calc
SPEX> plot
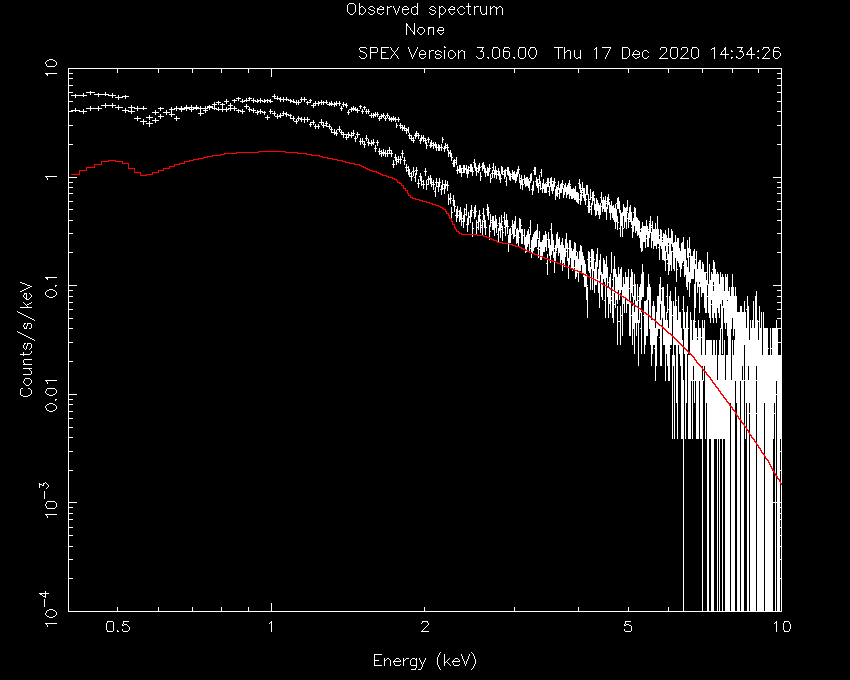
Now, the model spectrum is much closer to the best solution, so we can attempt a fit:
SPEX> fit
which provides the following best fit parameters:
SPEX> par show free
--------------------------------------------------------------------------------------------------
sect comp mod acro parameter with unit value status minimum maximum lsec lcom lpar
1 1 hot nh X-Column (1E28/m**2) 2.1649615E-04 thawn 0.0 1.00E+20
1 2 pow norm Norm (1E44 ph/s/keV) 2507.844 thawn 0.0 1.00E+20
1 2 pow gamm Photon index 1.496156 thawn -10. 10.
2 1 hot nh X-Column (1E28/m**2) 1.5288954E-04 thawn 0.0 1.00E+20
2 2 pow norm Norm (1E44 ph/s/keV) 1878.148 thawn 0.0 1.00E+20
2 2 pow gamm Photon index 2.292902 thawn -10. 10.
Instrument 1 region 1 has norm 1.00000E+00 and is frozen
Instrument 1 region 2 has norm 1.00000E+00 and is frozen
--------------------------------------------------------------------------------
Fluxes and restframe luminosities between 2.0000 and 10.000 keV
sect comp mod photon flux energy flux nr of photons luminosity
(phot/m**2/s) (W/m**2) (photons/s) (W)
1 2 pow 156.468 1.123012E-13 1.971041E+47 1.413442E+32
2 2 pow 41.1973 2.504328E-14 5.188680E+46 3.152038E+31
--------------------------------------------------------------------------------
Fit method : Classical Levenberg-Marquardt
Fit statistic : C-statistic
C-statistic : 1334.89
Expected C-stat : 1306.19 +/- 49.94
Chi-squared value : 1240.11
Degrees of freedom: 1272
W-statistic : 0.00
And plot:
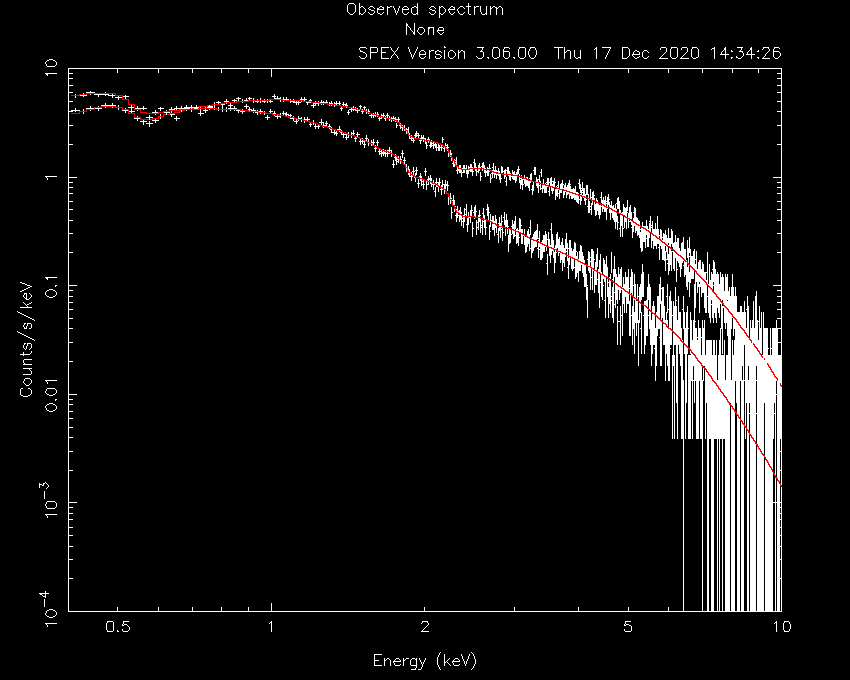
This fit already looks acceptable, but let’s assume that we want to test if the oxygen abundance in the absorber is consistent with solar. To do this, we can couple the oxygen abundances in the two hot models to each other:
SPEX> par 2 1 08 couple 1 1 08
SPEX> par 1 1 08 s t
SPEX> fit
SPEX> par show free
--------------------------------------------------------------------------------------------------
sect comp mod acro parameter with unit value status minimum maximum lsec lcom lpar
1 1 hot nh X-Column (1E28/m**2) 2.1453765E-04 thawn 0.0 1.00E+20
1 1 hot 08 Abundance O 1.083166 thawn 0.0 1.00E+10
1 2 pow norm Norm (1E44 ph/s/keV) 2509.920 thawn 0.0 1.00E+20
1 2 pow gamm Photon index 1.496786 thawn -10. 10.
2 1 hot nh X-Column (1E28/m**2) 1.5155401E-04 thawn 0.0 1.00E+20
2 1 hot 08 Abundance O 1.083166 frozen 0.0 1.00E+10 1 1 08
2 2 pow norm Norm (1E44 ph/s/keV) 1879.305 thawn 0.0 1.00E+20
2 2 pow gamm Photon index 2.293384 thawn -10. 10.
Instrument 1 region 1 has norm 1.00000E+00 and is frozen
Instrument 1 region 2 has norm 1.00000E+00 and is frozen
--------------------------------------------------------------------------------
Fluxes and restframe luminosities between 2.0000 and 10.000 keV
sect comp mod photon flux energy flux nr of photons luminosity
(phot/m**2/s) (W/m**2) (photons/s) (W)
1 2 pow 156.456 1.122785E-13 1.970944E+47 1.413182E+32
2 2 pow 41.1969 2.504092E-14 5.188782E+46 3.151799E+31
--------------------------------------------------------------------------------
Fit method : Classical Levenberg-Marquardt
Fit statistic : C-statistic
C-statistic : 1334.81
Expected C-stat : 1306.19 +/- 49.94
Chi-squared value : 1239.62
Degrees of freedom: 1273
W-statistic : 0.00
The example above shows that we can couple parameters across sectors to each other and fit them. Although this may not be a realistic science case, it shows how fitting two different spectra simultaneously can be done and how parameters of different models can be coupled to each other.
By the way, the oxygen abundance in this example did not turn out to be significantly different from solar when one calculates the error on oxygen:
SPEX> error 1 1 08
parameter C-stat Delta Delta
value value parameter C-stat
----------------------------------------------------
0.838682 1335.33 -0.244484 0.52
0.594198 1336.85 -0.488968 2.03
0.838682 1335.33 -0.244484 0.52
0.761005 1335.70 -0.322161 0.89
0.739144 1335.82 -0.344022 1.01
0.741589 1335.81 -0.341577 0.99
1.32765 1335.17 0.244484 0.36
1.57213 1336.28 0.488968 1.46
1.41755 1335.50 0.334387 0.69
1.48019 1335.78 0.397026 0.97
1.48650 1335.82 0.403330 1.00
Parameter 1 1 08 : 1.0832 Errors: -0.34158 , 0.40333
