2.1. Fitting a CCD spectrum¶
2.1.1. Goal¶
To load and fit a CCD spectrum (e.g. MOS1 aboard XMM-Newton) into SPEX.
2.1.2. Preparation¶
To be able to fit a spectrum, you need a spectrum and response file in SPEX format. To convert spectra from OGIP
format (e.g. pha, arf, rmf) to SPEX format, please use the trafo program like described in How to convert spectra to SPEX format.
If you have the Pyspextools package installed, then you can use
ogip2spex as an alternative to trafo.
Using the commands above, you can obtain a .spo and .res file containing your spectrum. To follow this thread, you
can also download example files here: mos.spo and mos.res.
2.1.3. Starting SPEX¶
The SPEX program is started by entering spex in a linux terminal window. In the following sections we describe
one run of the program. To start SPEX do this:
user@linux:~> spex
Welcome user to SPEX version 3.06.00
SPEX>
If SPEX does not run, please check if you set the SPEX90 variable right and sourced spexdist.(c)sh
as explained in How to install SPEX.
2.1.4. Loading data¶
Then, we have to load the data files. This is done using the data command (Data: read response file and spectrum). It is a general thing
in SPEX that filename extensions are not typed explicitly when issuing a command. If you have a file called
mos.spo and mos.res then you type:
SPEX> data mos mos
The response file (mos.res) is entered first and then the file containing the spectrum (mos.spo). You can avoid
confusion by giving the same filename to both .res and .spo files. Remember that the order of the words in the commands
is very important!
2.1.5. Plot the data¶
It really helps to see the spectrum while we are working on it, so we need a plot window and tell spex that we want to see a plot of the data. (Note that the text after the # is a comment and should not be copied on the command line).
SPEX> plot dev xs # Open plot device `X server`
SPEX> plot type data # Choose the plot type `data`
SPEX> plot
The commands above open a PGPLOT window and set the plot type to data, which means that the observed spectrum
and the model (folded through the response matrix) will be shown. The last plot command tells SPEX to
refresh the plot.
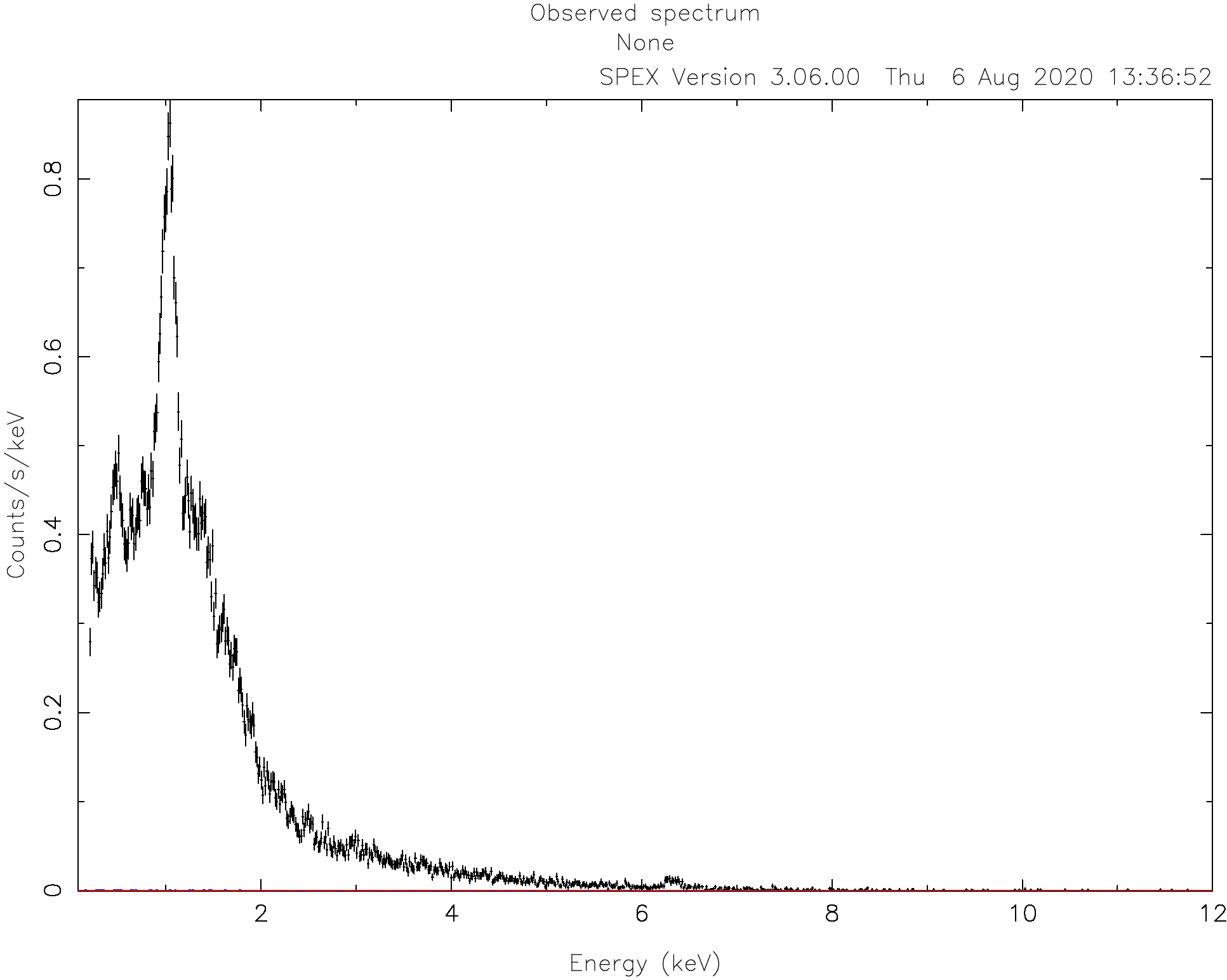
Usually CCD spectra benefit from a logarithmic scale on both the X and Y axes:
SPEX> plot x log
SPEX> plot y log
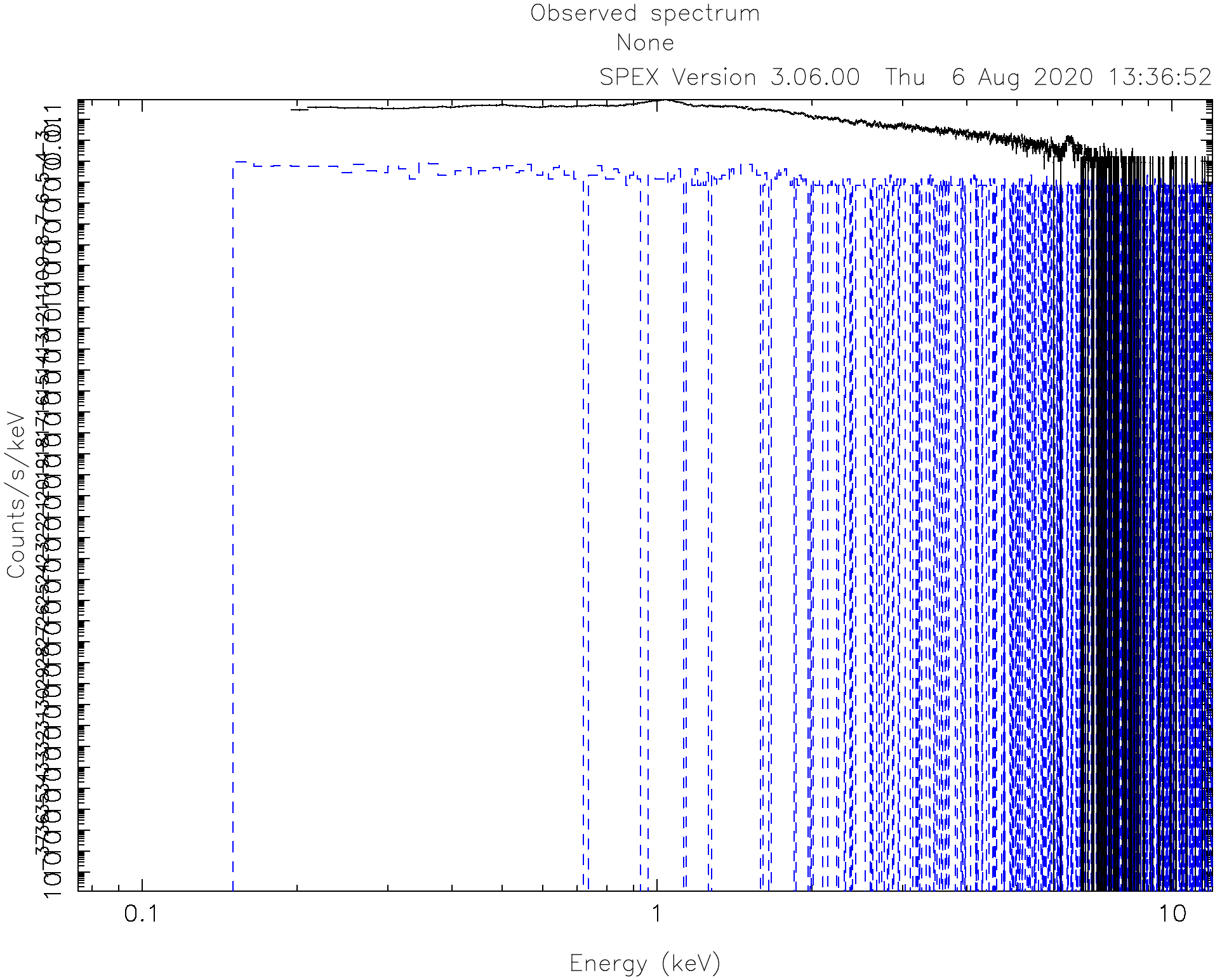
By default, the ranges of the axes are usually too broad. For this spectrum, the X axis range is good between 0.1 and 10 keV and the Y axis range between 1E-4 and 10.
SPEX> plot rx 0.1:10.
SPEX> plot ry 1E-4:10.
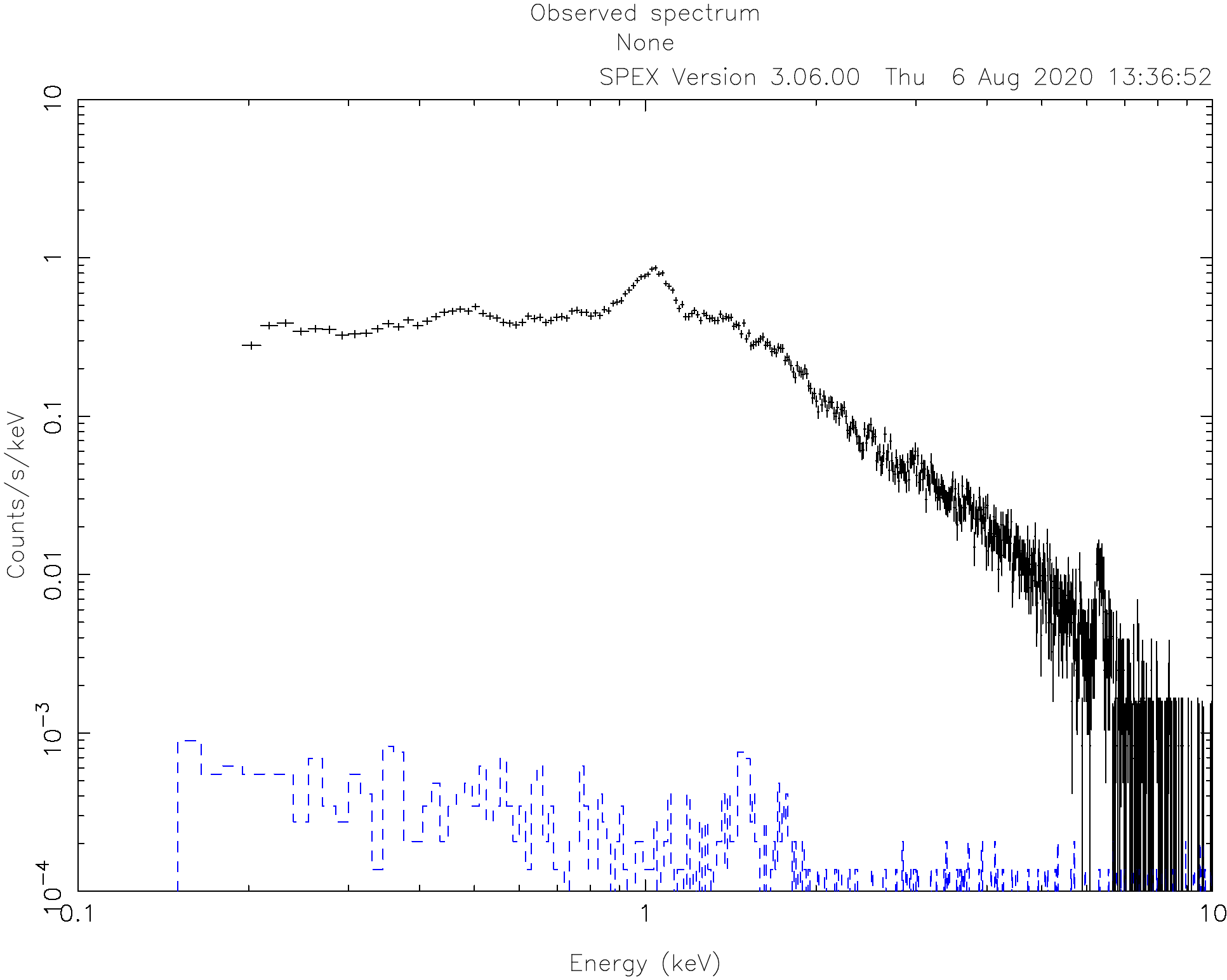
2.1.6. Select good data and bin the spectrum¶
Before we start fitting, we can make sure that only trustworthy data is fitted. For MOS1, for example, we know that
the calibration is valid for the energy range between roughly 0.3 keV and 10 keV. To fit only the good spectral
interval, we need to ignore the parts at low and high energies. This is done using the ignore command.
In addition, we can bin the spectrum. To automatically rebin to the recommended (optimal) bin size, one can use
the obin command. This command bins the spectrum optimally based on the instrument resolution and statistics.
SPEX> ignore 0:0.3 unit kev
SPEX> ignore 10:100 unit kev
SPEX> obin 0.3:10 unit kev
SPEX> plot

2.1.7. Define the model¶
Next we can define the model that we want to fit. In this case, we are looking at a MOS spectrum of a
galaxy cluster. The simplest model that we can try is a single temperature spectrum absorbed by gas in
the ISM. We also add a redshift component reds (Reds: redshift model) to shift the energy of the model
spectrum with the right amount:
SPEX> com reds
You have defined 1 component.
SPEX> com hot
You have defined 2 components.
SPEX> com cie
You have defined 3 components.
The hot model (Hot: collisional ionisation equilibrium absorption model) is actually a gas in equilibrium in absorption, which is a fair representation of
the neutral gas phase of the ISM. Later we will put the temperature of this component to keV
to emulate a neutral plasma.
The cie model (Cie: collisional ionisation equilibrium model) represents a single temperature plasma in collisional ionisation equilibrium,
which is commonly used for clusters.
Then the components need to be related to each other, which means you need to specify how the multiplicative models should be applied to the additive models. The multiplicative components should be listed in order from the source to the observer (see also Comp: create, delete and relate spectral components):
SPEX> com rel 3 1,2
This means that the emitted CIE component (#3) will be first redshifted by component #1 and then absorbed by component #2. If you have multiple additive components, this should be done for each one. It is possible to supply a range of components.
SPEX> calc
SPEX> plot
Calculating and plotting the model unsurprisingly results in a curve that is not near to the data.
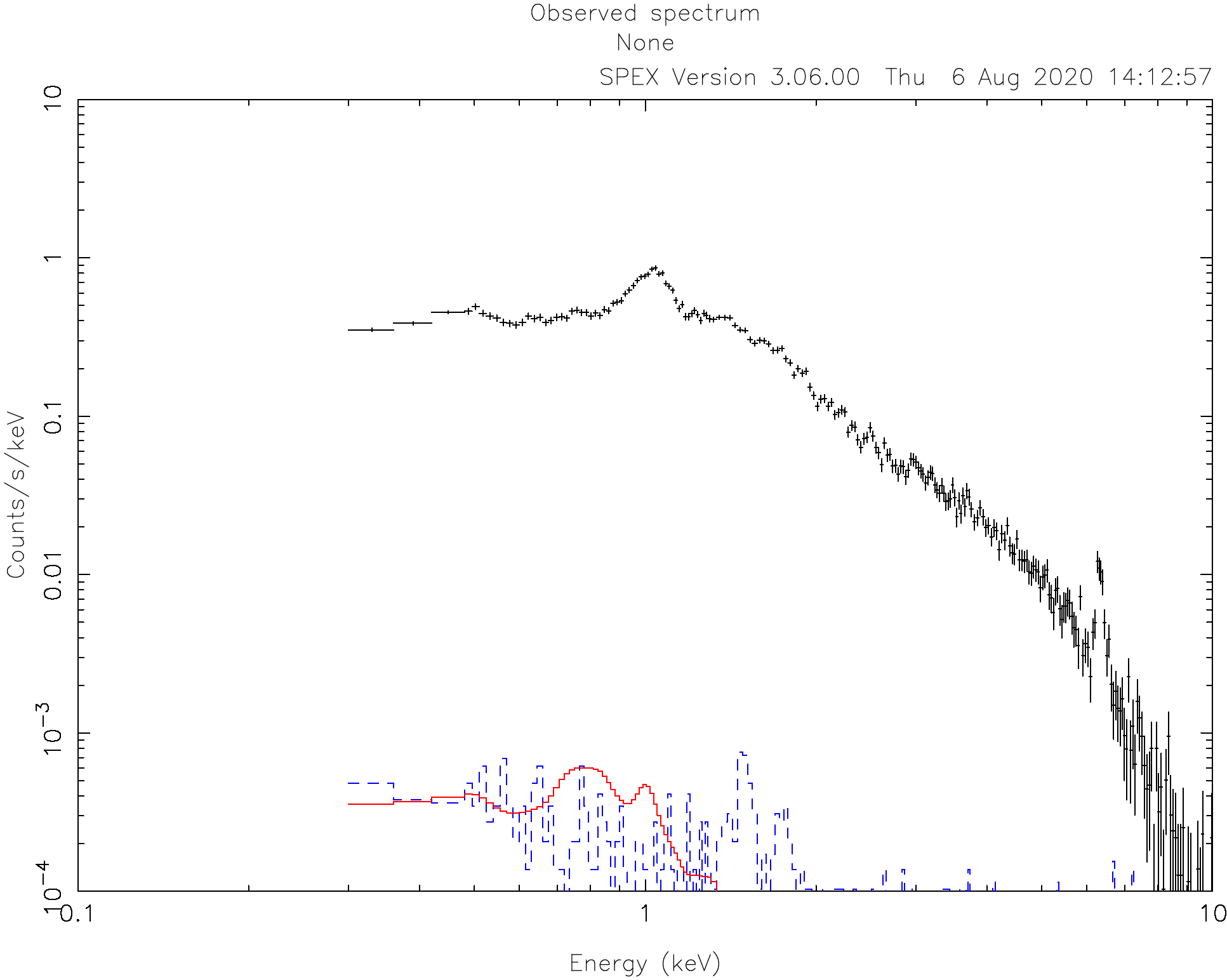
2.1.8. Initial guess of parameters¶
To help the spectral fitting process, it is good to provide initial guesses for the model parameters. This way, the spectral fit starts already with a model that is in the right direction. As a more experienced user, you usually have a rough idea what the parameters should be by looking at the raw spectrum. For this cluster, for example, the redshift is around 0.05, the absorption column is small, and the temperature of the cluster is around 3 keV. We can set the guess parameters as follows:
SPEX> par 1 1 z v 0.05
SPEX> par 1 1 z s t
SPEX> par 1 2 t v 8E-6
SPEX> par 1 2 t s f
SPEX> par 1 2 nh v 1E-4
SPEX> par 1 3 norm v 1000.
SPEX> par 1 3 t v 3.0
SPEX> ca
SPEX> pl
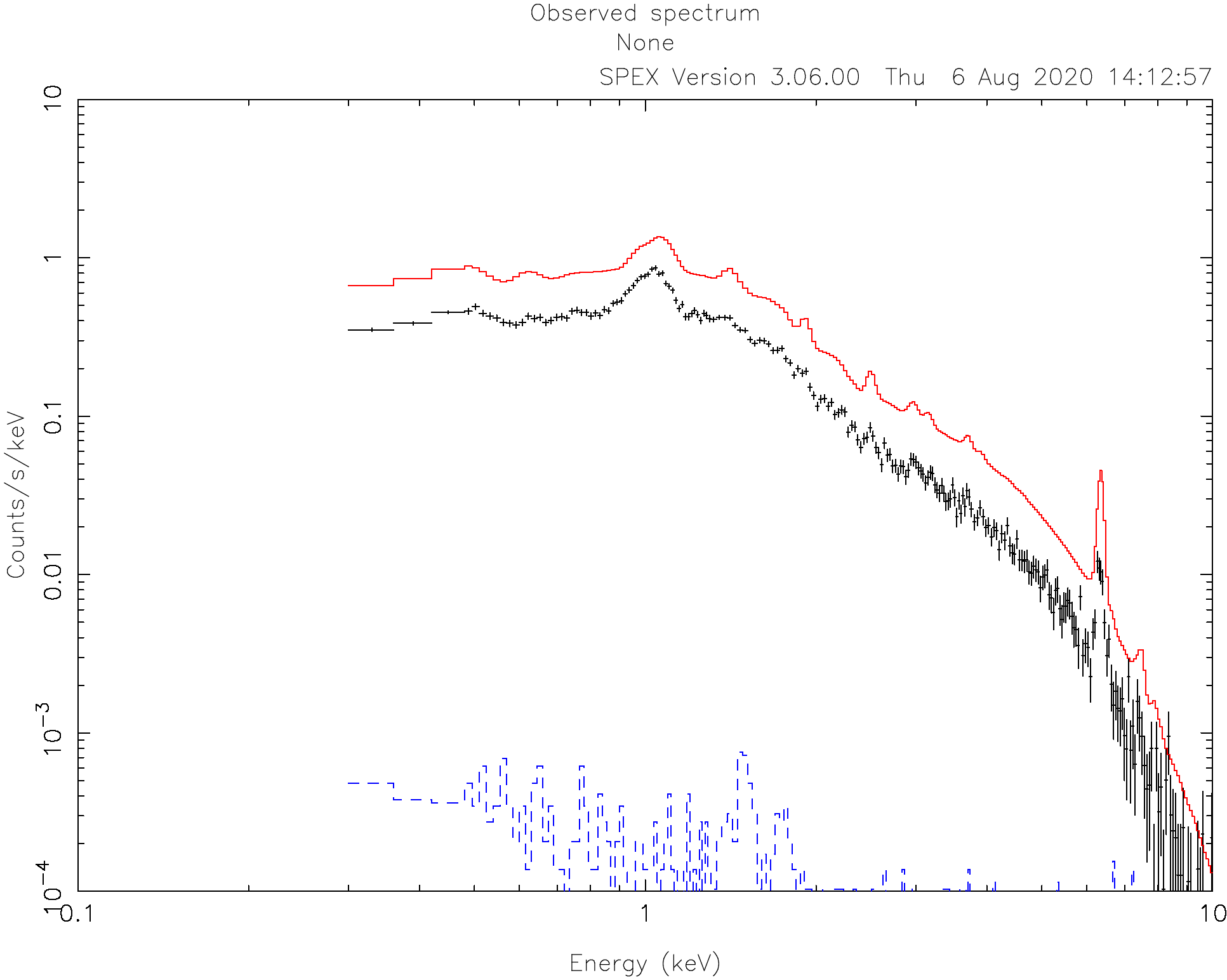
As we can see from the image, the first guess of the model is already in the right direction.
In this example, we assume that the exact redshift is unknown. However, if you do have an accurate measurement of the distance, it is wise to set that distance in SPEX (Distance: set the source distance):
SPEX> dist 0.05 z
The command above sets the distance to 0.05 z and makes sure that the luminosities are correctly calculated. Note that this distance change also affects the values of the normalisation of the models! So, we increase the normalisation to keep the model reasonably close to the data:
SPEX> par 1 3 norm v 1E+8
2.1.9. Fit the model¶
We are now ready to fit the spectrum. To see the fitting steps, we can give the command fit print 1. This needs
to be set only once per session. A subsequent fit command (Fit: spectral fitting) starts to optimize the parameters:
SPEX> fit print 1
SPEX> fit
42102.6 5 5.000E-02 1.000E-04 1.000E+08 3.00
2461.87 10 5.404E-02 9.087E-05 2.021E+08 2.04
428.533 15 5.439E-02 1.041E-04 2.412E+08 2.31
414.925 20 5.437E-02 9.425E-05 2.429E+08 2.37
414.651 25 5.426E-02 9.229E-05 2.428E+08 2.37
414.532 30 5.408E-02 9.269E-05 2.428E+08 2.37
414.525 35 5.412E-02 9.281E-05 2.428E+08 2.37
414.524 42 5.411E-02 9.270E-05 2.428E+08 2.37
414.524 48 5.411E-02 9.265E-05 2.428E+08 2.37
--------------------------------------------------------------------------------------------------
sect comp mod acro parameter with unit value status minimum maximum lsec lcom lpar
1 1 reds z Redshift 5.4108180E-02 thawn -1.0 1.00E+10
1 1 reds flag Flag: cosmo=0, vel=1 0.000000 frozen 0.0 1.0
1 2 hot nh X-Column (1E28/m**2) 9.2653019E-05 thawn 0.0 1.00E+20
1 2 hot t Temperature (keV) 1.9999999E-04 frozen 2.00E-04 1.00E+03
1 2 hot rt T(balance) / T(spec) 1.000000 frozen 1.00E-04 1.00E+04
1 2 hot fcov Covering fraction 1.000000 frozen 0.0 1.0
1 2 hot v RMS Velocity (km/s) 100.0000 frozen 0.0 3.00E+05
1 2 hot rms RMS blend (km/s) 0.000000 frozen 0.0 1.00E+05
1 2 hot dv Vel. separ. (km/s) 100.0000 frozen 0.0 1.00E+05
1 2 hot zv Average vel. (km/s) 0.000000 frozen -1.00E+05 1.00E+05
1 2 hot ref Reference atom 1.000000 frozen 1.0 30.
1 2 hot 01 Abundance H 1.000000 frozen 0.0 1.00E+10
1 2 hot 02 Abundance He 1.000000 frozen 0.0 1.00E+10
1 2 hot 03 Abundance Li 1.000000 frozen 0.0 1.00E+10
1 2 hot 04 Abundance Be 1.000000 frozen 0.0 1.00E+10
1 2 hot 05 Abundance B 1.000000 frozen 0.0 1.00E+10
1 2 hot 06 Abundance C 1.000000 frozen 0.0 1.00E+10
1 2 hot 07 Abundance N 1.000000 frozen 0.0 1.00E+10
1 2 hot 08 Abundance O 1.000000 frozen 0.0 1.00E+10
1 2 hot 09 Abundance F 1.000000 frozen 0.0 1.00E+10
1 2 hot 10 Abundance Ne 1.000000 frozen 0.0 1.00E+10
1 2 hot 11 Abundance Na 1.000000 frozen 0.0 1.00E+10
1 2 hot 12 Abundance Mg 1.000000 frozen 0.0 1.00E+10
1 2 hot 13 Abundance Al 1.000000 frozen 0.0 1.00E+10
1 2 hot 14 Abundance Si 1.000000 frozen 0.0 1.00E+10
1 2 hot 15 Abundance P 1.000000 frozen 0.0 1.00E+10
1 2 hot 16 Abundance S 1.000000 frozen 0.0 1.00E+10
1 2 hot 17 Abundance Cl 1.000000 frozen 0.0 1.00E+10
1 2 hot 18 Abundance Ar 1.000000 frozen 0.0 1.00E+10
1 2 hot 19 Abundance K 1.000000 frozen 0.0 1.00E+10
1 2 hot 20 Abundance Ca 1.000000 frozen 0.0 1.00E+10
1 2 hot 21 Abundance Sc 1.000000 frozen 0.0 1.00E+10
1 2 hot 22 Abundance Ti 1.000000 frozen 0.0 1.00E+10
1 2 hot 23 Abundance V 1.000000 frozen 0.0 1.00E+10
1 2 hot 24 Abundance Cr 1.000000 frozen 0.0 1.00E+10
1 2 hot 25 Abundance Mn 1.000000 frozen 0.0 1.00E+10
1 2 hot 26 Abundance Fe 1.000000 frozen 0.0 1.00E+10
1 2 hot 27 Abundance Co 1.000000 frozen 0.0 1.00E+10
1 2 hot 28 Abundance Ni 1.000000 frozen 0.0 1.00E+10
1 2 hot 29 Abundance Cu 1.000000 frozen 0.0 1.00E+10
1 2 hot 30 Abundance Zn 1.000000 frozen 0.0 1.00E+10
1 2 hot file File electr.distrib.
1 3 cie norm ne nX V (1E64/m**3) 2.4279381E+08 thawn 0.0 1.00E+20
1 3 cie t Temperature (keV) 2.372914 thawn 5.00E-04 1.00E+03
1 3 cie sig Sigma 0.000000 frozen 0.0 1.00E+04
1 3 cie sup Sigma up 0.000000 frozen 0.0 1.00E+04
1 3 cie logt T grid (lin/log) 1.000000 frozen 0.0 1.0
1 3 cie ed El dens (1E20/m**3) 9.9999998E-15 frozen 1.00E-22 1.00E+10
1 3 cie it Ion temp (keV) 1.000000 frozen 1.00E-04 1.00E+07
1 3 cie rt T(balance) / T(spec) 1.000000 frozen 1.00E-04 1.00E+04
1 3 cie vrms RMS Velocity (km/s) 0.000000 frozen 0.0 3.00E+05
1 3 cie ref Reference atom 1.000000 frozen 1.0 30.
1 3 cie 01 Abundance H 1.000000 frozen 0.0 1.00E+10
1 3 cie 02 Abundance He 1.000000 frozen 0.0 1.00E+10
1 3 cie 03 Abundance Li 1.000000 frozen 0.0 1.00E+10
1 3 cie 04 Abundance Be 1.000000 frozen 0.0 1.00E+10
1 3 cie 05 Abundance B 1.000000 frozen 0.0 1.00E+10
1 3 cie 06 Abundance C 1.000000 frozen 0.0 1.00E+10
1 3 cie 07 Abundance N 1.000000 frozen 0.0 1.00E+10
1 3 cie 08 Abundance O 1.000000 frozen 0.0 1.00E+10
1 3 cie 09 Abundance F 1.000000 frozen 0.0 1.00E+10
1 3 cie 10 Abundance Ne 1.000000 frozen 0.0 1.00E+10
1 3 cie 11 Abundance Na 1.000000 frozen 0.0 1.00E+10
1 3 cie 12 Abundance Mg 1.000000 frozen 0.0 1.00E+10
1 3 cie 13 Abundance Al 1.000000 frozen 0.0 1.00E+10
1 3 cie 14 Abundance Si 1.000000 frozen 0.0 1.00E+10
1 3 cie 15 Abundance P 1.000000 frozen 0.0 1.00E+10
1 3 cie 16 Abundance S 1.000000 frozen 0.0 1.00E+10
1 3 cie 17 Abundance Cl 1.000000 frozen 0.0 1.00E+10
1 3 cie 18 Abundance Ar 1.000000 frozen 0.0 1.00E+10
1 3 cie 19 Abundance K 1.000000 frozen 0.0 1.00E+10
1 3 cie 20 Abundance Ca 1.000000 frozen 0.0 1.00E+10
1 3 cie 21 Abundance Sc 1.000000 frozen 0.0 1.00E+10
1 3 cie 22 Abundance Ti 1.000000 frozen 0.0 1.00E+10
1 3 cie 23 Abundance V 1.000000 frozen 0.0 1.00E+10
1 3 cie 24 Abundance Cr 1.000000 frozen 0.0 1.00E+10
1 3 cie 25 Abundance Mn 1.000000 frozen 0.0 1.00E+10
1 3 cie 26 Abundance Fe 1.000000 frozen 0.0 1.00E+10
1 3 cie 27 Abundance Co 1.000000 frozen 0.0 1.00E+10
1 3 cie 28 Abundance Ni 1.000000 frozen 0.0 1.00E+10
1 3 cie 29 Abundance Cu 1.000000 frozen 0.0 1.00E+10
1 3 cie 30 Abundance Zn 1.000000 frozen 0.0 1.00E+10
1 3 cie file File electr.distrib.
1 3 cie x1 T1/T0 1.000000 frozen 1.0 1.00E+10
1 3 cie y1 N1/N0 0.000000 frozen 0.0 1.00E+10
Instrument 1 region 1 has norm 1.00000E+00 and is frozen
--------------------------------------------------------------------------------
Fluxes and restframe luminosities between 2.0000 and 10.000 keV
sect comp mod photon flux energy flux nr of photons luminosity
(phot/m**2/s) (W/m**2) (photons/s) (W)
1 3 cie 4.13667 2.229383E-15 2.655905E+51 1.422295E+36
--------------------------------------------------------------------------------
Fit method : Classical Levenberg-Marquardt
Fit statistic : C-statistic
C-statistic : 414.52
Expected C-stat : 247.13 +/- 21.92
Chi-squared value : 528.16
Degrees of freedom: 239
W-statistic : 0.00
At the end of the optimization step, SPEX prints out an overview of the fit parameters and the fit statistics. Here we can see that the fit improved, but there is still room for improvement.
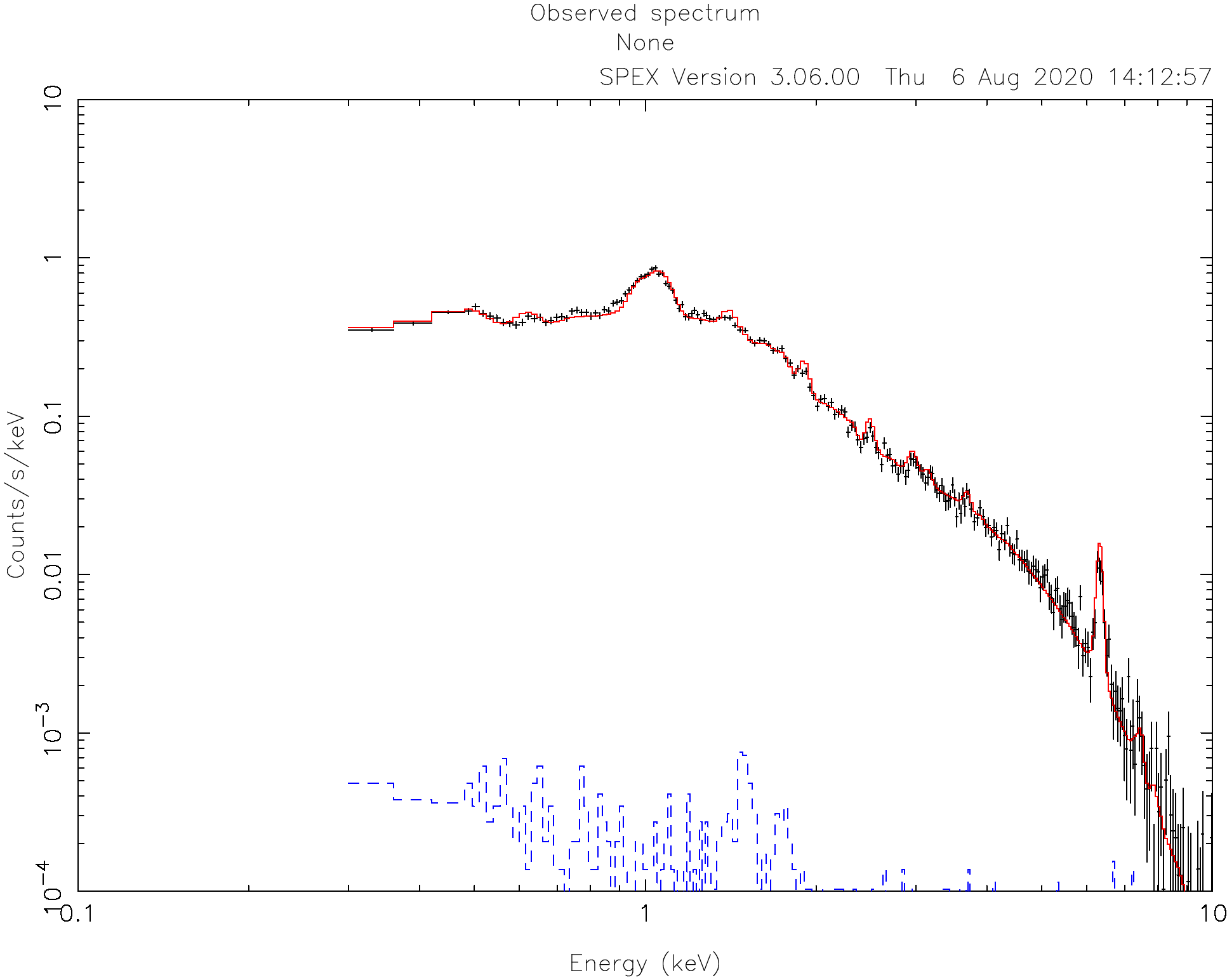
2.1.10. Fitting abundances¶
Although the C-statistics are not too bad, there are still residuals in the spectrum, especially around the strongest spectral lines. This is because the metal abundances in the gas are still fixed to 1.0. We can let the abundances vary in the optimization by setting them to thawn:
SPEX> par 1 3 08 s t
SPEX> par 1 3 12 s t
SPEX> par 1 3 14 s t
SPEX> par 1 3 16 s t
SPEX> par 1 3 18 s t
SPEX> par 1 3 20 s t
SPEX> par 1 3 26 s t
SPEX> par 1 3 28 s t
SPEX> fit
The optimization leads to an even better fit:
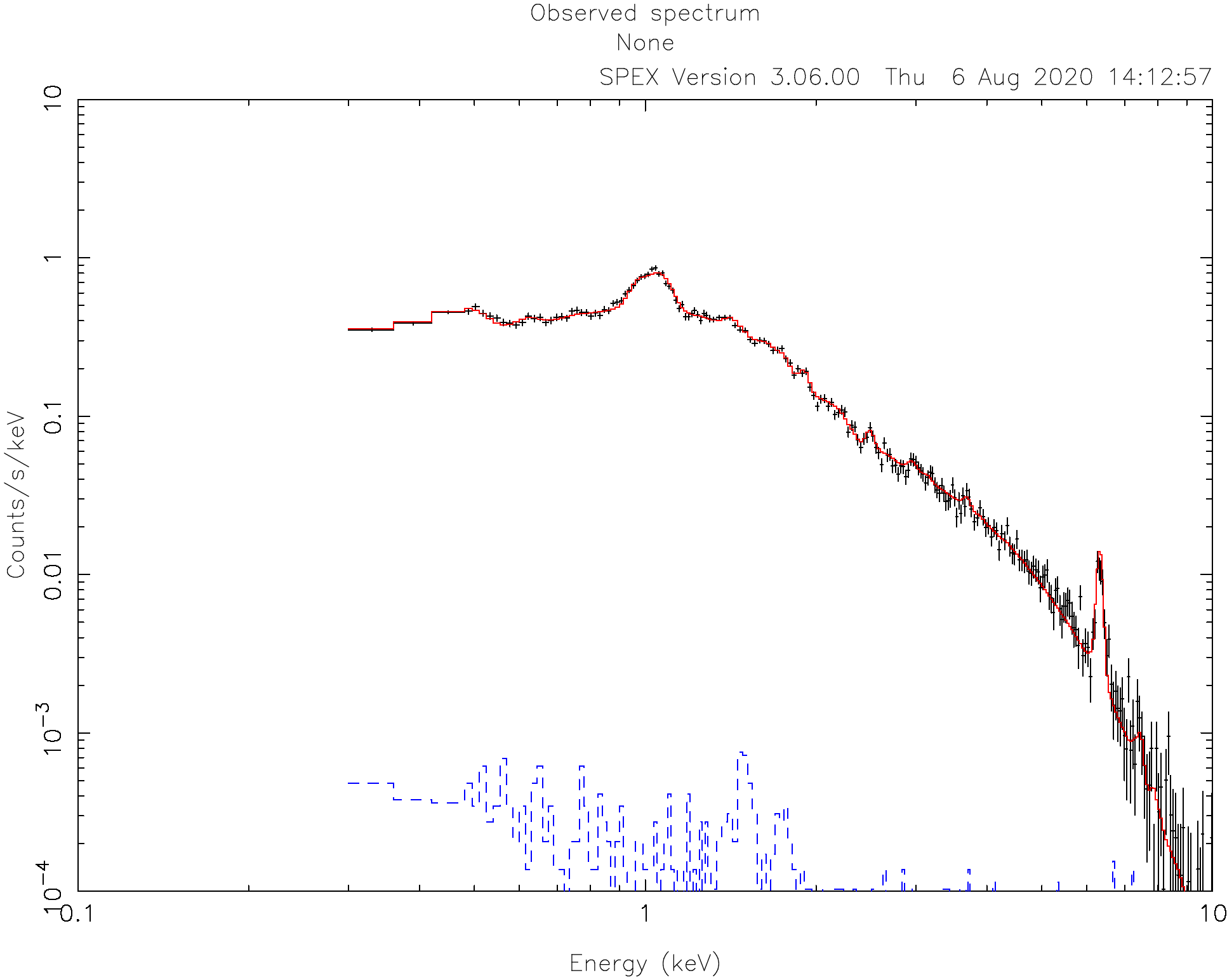
Fit method : Classical Levenberg-Marquardt
Fit statistic : C-statistic
C-statistic : 266.80
Expected C-stat : 247.12 +/- 21.91
Chi-squared value : 366.77
Degrees of freedom: 231
W-statistic : 0.00
2.1.11. Calculating errors¶
When we have the best fit, we can calculate the errors (Error: Calculate the errors of the fitted parameters). This has to be done per parameter. Below we calculate, for example, the error on the best fit temperature:
SPEX> error 1 3 t
parameter C-stat Delta Delta
value value parameter C-stat
----------------------------------------------------
2.33348 267.68 -2.246547E-02 0.89
2.31101 270.23 -4.493093E-02 3.44
2.33348 267.68 -2.246547E-02 0.89
2.33247 267.69 -2.346587E-02 0.90
2.32425 268.52 -3.169394E-02 1.73
2.32836 268.05 -2.758002E-02 1.26
2.33042 267.87 -2.552295E-02 1.07
2.33127 267.79 -2.466774E-02 1.00
2.37841 267.71 2.246547E-02 0.92
2.40087 270.28 4.493093E-02 3.49
2.37841 267.71 2.246547E-02 0.92
2.37914 267.77 2.319646E-02 0.98
2.37940 267.78 2.345586E-02 0.99
2.37974 267.81 2.379751E-02 1.02
Parameter 1 3 t : 2.3559 Errors: -2.46677E-02 , 2.37975E-02
The error command reports the best fit value for the temperature and the lower and upper 1 sigma (68%) confidence level.
Usually, the error calculation stage is the end point of a spectral analysis. In this example, we can quit SPEX now:
SPEX> quit
Thank you for using SPEX!
